人教A版高中数学必修二平面向量的概念教学设计
-
- 页数:4页
- 字数:约 2795 字
- 大小:215.50KB
- 格式:.doc
- 版本:Office2016及以上版本
- 作者:白家安毓设计
平面向量的概念教学设计

课题
6.1平面向量的概念
单元
第六单元
学科
数学
年级
高一
教材分析
本节内容是平面向量的概念,由物理中的路程和位移情境导入,学习平面向量的概念、表示以及平面向量之间的关系这些知识点,为平面向量的运算做铺垫。
教学目标与核心素养
1.数学抽象:利用位移和路程的相关情境将平面向量具体化;
2.逻辑推理:通过课堂探究逐步培养学生的逻辑思维能力.
3.数学建模:掌握平面向量的相关知识,为空间向量的学习打好基础的同时,也能学习利用向量解决实际问题。
4.直观想象:通过有向线段直观判断平面向量之间的关系;
5.数学运算:能够正确判断平面向量之间的关系;
6.数据分析:通过经历提出问题—推导过程—得出结论—例题讲解—练习巩固的过程,让学生认识到数学知识的逻辑性和严密性。
重点
平面向量的概念;平面向量的表示;平面向量之间的关系。
难点
平面向量的表示;平面向量之间的关系。
教学过程
教学环节
教师活动
学生活动
设计意图
导入新课
情境导入:
情境一:小船由A地航行15 n mile 到达B地。试问小船能到达B地吗?
情境二:小船由A地向东南方向航行15 n mile 到达B地。试问小船能到达B地吗?
问:位移和距离这两个量有什么不同?
情境三:物体受到的重力是竖直向下的,物体的质量越大,它受到的重力越大。
情境四:物体在液体中受到的浮力是竖直向上的,物体浸在液体中的体积越大,它受到的浮力越大。问:你能通过这些物理量得出向量的概念吗?
学生思考问题,引出本节新课内容。
设置问题情境,激发学生学习兴趣,并引出本节新课。
讲授新课
知识探究(一):向量的概念
定义:既有大小又有方向的量统称为向量。把只有大小没有方向的量称为数量,如年龄、身高、长度、面积、体积、质量等。
注:1.向量两要素:大小,方向
2.向量与数量的区别:
①数量只有大小,可以比较大小。
②向量有方向,大小双重属性,而方向是不能比较大小的,因此向量不能比较大小。
知识链接:物理学中常称向量为矢量,数量为标量。你还能举出物理学中的一些向量和数量吗?
练习一:在质量、重力、速度、加速度、身高、面积、体积这些量中,_____________是数量_______________是向量.
练习二:
1.身高是一个向量( )
2.温度含零上和零下温度,所以温度是向量( )
3.坐标平面上的 x 轴和 y 轴都是向量。( )
知识探究(二):向量的表示思考:对于一个实数,可以用数轴上的点表示,而且不同的点表示不同的数量。那么,该如何表示向量呢?
思考:根据情景二,你发现位移是怎样表示的?向量怎样表示?
几何表示法:
用有向线段表示向量,长度表示向量的大小,箭头所指的方向表示向量的方向。
有向线段三要素:起点、方向、长度。
问:有向线段是向量,向量就是有向线段。这种说法对吗?
思考:你能用表示线段的方法表示向量吗?向量的大小和方向怎样表示?
字母表示法:大写字母和小写字母。
箭头表示向量的方向,线段的长度表示大小。
知识探究(三):向量的模和两类特殊向量
思考:有什么含义?
向量的模:向量的大小称为向量的长度(或称为模),记作||.
两类特殊向量:零向量和单位向量。
思考:1. 与0有区别吗?为什么?
2. 零向量和单位向量的方向呢?
3. 平面直角坐标系内,起点在原点的单位向量,它们的终点的轨迹是什么图形?
判断
1.向量的模是一个正实数。( )
2.若|a|>|b| ,则a > b。 ( )
注:向量不能比较大小
例1. 如图,分别用向量表示A地至B、C两地的位移,并根据图中的比例尺,求出A地至B,C两地的实际距离(精确到1km)
知识探究(四):向量之间的关系
思考:观察图象,探究发现平行向量。
平行向量:方向相同或相反的 叫做平行向量. 记作 //.
共线向量:平行向量又称为共线向量.
思考:是相同的向量吗?
由此得出相等向量和相反向量的定义。
1.若非零向量AB//CD ,那么AB//CD吗?
2.若a//b ,则a与b的方向一定相同或相反吗?
3.相等向量一定是平行向量吗?
平行向量一定是相等向量吗?
例2 已知O为正六边形ABCDEF的中心,在图中所标出的向量中:
(1)写出图中的共线向量;
(2)分别写出图中与 相等的向量;
提升训练
1、回答下列问题:
(1)平行向量是否一定方向相同?
(2)不相等的向量是否一定不平行?
(3)与零向量相等的向量必定是什么向量?
学生根据两个情境,探究平面向量的概念。
学生根据环环相扣的思考题,探究平面向量的表示。
学生根据动态变化图,观察探究的出向量之间的关系。
利用例题引导学生掌握本节课知识,并能够灵活运用.
学生和教师共同探究完成3个练习题。
利用两个情境探究得出平面向量的概念,培养学生探索的精神.
通过思考,培养学生探索新知的精神和能力.
利用数形结合的思想,化抽象为具体,提高学生的抽象能力和逻辑思维能力。
例题的3问三种类型,加深学生对基础知识理解,并能够灵活运用基础知识解决具体问题。
通过这3个题,巩固基础知识,发散学生思维,培养学生思维的严谨性和对数学的探索精神。
您可能喜欢的文档
查看更多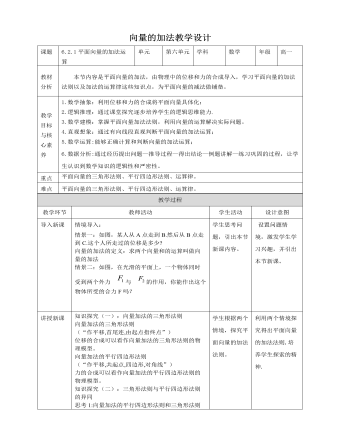
人教A版高中数学必修二向量的加法教学设计
- 页数:4页
- |大小:317.50KB

人教A版高中数学必修一对数的概念教学设计(2)
- 页数:5页
- |大小:110.37KB

人教A版高中数学必修一函数的概念教学设计(1)
- 页数:10页
- |大小:235.84KB

人教A版高中数学必修一函数的概念教学设计(2)
- 页数:9页
- |大小:196.78KB

人教A版高中数学必修一集合的概念教学设计(2)
- 页数:9页
- |大小:160.49KB

人教A版高中数学必修二平面教学设计
- 页数:8页
- |大小:251.00KB
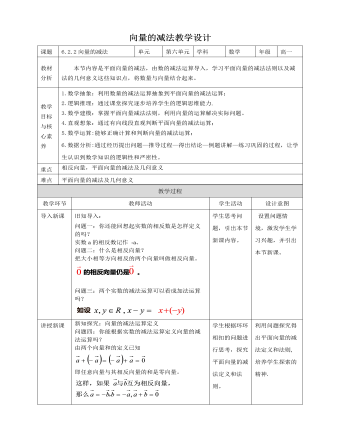
人教A版高中数学必修二向量的减法运算教学设计
- 页数:6页
- |大小:268.00KB
热门课件教案

XX区文旅体局2023年工作总结 及2024年工作安排
- 页数:8页
- |大小:32.41KB
- 课件教案

XX区民政局党支部开展主题教育工作情况总结报告
- 页数:3页
- |大小:24.47KB
- 课件教案

交通运输局在巡回指导组主题教育阶段性工作总结推进会上的汇报发言
- 页数:4页
- |大小:33.41KB
- 课件教案

2023年区实施乡村振兴战略工作总结
- 页数:6页
- |大小:27.90KB
- 课件教案

关于2024年上半年工作总结和下半年工作计划
- 页数:5页
- |大小:29.72KB
- 课件教案

县综合行政执法局2023年工作总结和2024年工作计划
- 页数:8页
- |大小:28.37KB
- 课件教案
今日更新

5月份主题教育工作情况总结汇报
- 页数:3页
- |大小:136.87KB

××县招商局2024年上半年工作总结
- 页数:12页
- |大小:142.54KB

×××公安局机关党委上半年党建工作总结
- 页数:7页
- |大小:186.25KB

《2019—2024年全国党政领导班子建设规划纲要》实施情况的工作总结3800字
- 页数:6页
- |大小:29.16KB

“转观念、勇担当、新征程、创一流”主题教育活动阶段性工作总结
- 页数:3页
- |大小:22.76KB

“四零”承诺服务创建工作总结
- 页数:5页
- |大小:39.83KB











