搜PPT搜文档
当前位置：首页 > Word文档 > 教育教学 > 课件教案> 【高教版】中职数学拓展模块：1.3《正弦定理与余弦定理》教案

【高教版】中职数学拓展模块：1.3《正弦定理与余弦定理》教案

  • 页数：8页
  • 字数：约 3578 字
  • 大小：218.41KB
  • 格式：.docx
  • 版本：Office2016及以上版本
  • 作者：陈杰出品
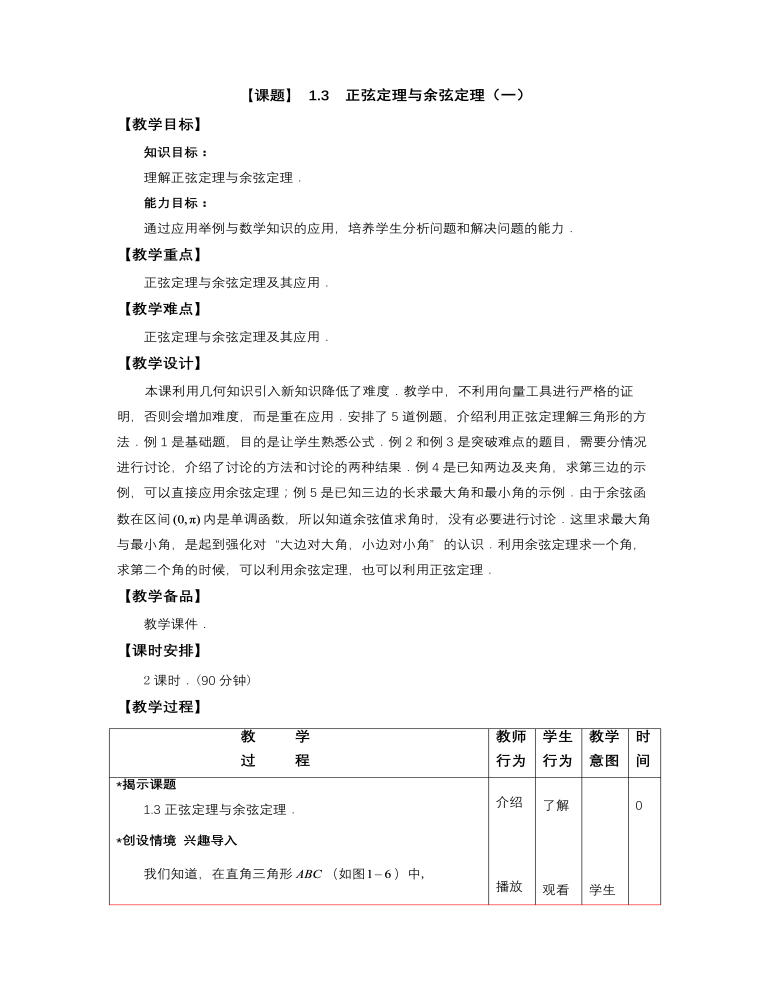
  • 【高教版】中职数学拓展模块：1.3《正弦定理与余弦定理》教案【高教版】中职数学拓展模块：1.3《正弦定理与余弦定理》教案【高教版】中职数学拓展模块：1.3《正弦定理与余弦定理》教案
  • 教 学 过 程教师 行为学生 行为教学 意图时间 *揭示课题 1.3正弦定理与余弦定理． *创设情境 兴趣导入 我们知道，在直角三角形（如图）中,,，即 ，， 由于,所以，于是 . 图1－6 所以 . 介绍 播放 课件 质疑 了解 观看 课件 思考 学生自然的走向知识点 0 10*动脑思考 探索新知 在任意三角形中，是否也存在类似的数量关系呢？ c 图1－7 当三角形为钝角三角形时，不妨设角为钝角，如图所示，以为原点，以射线的方向为轴正方向，建立直角坐标系，则 两边取与单位向量的数量积，得 由于设与角A，B，C相对应的边长分别为a，b，c，故 即 所以 同理可得 即 当三角形为锐角三角形时，同样可以得到这个结论.于是得到正弦定理： 在三角形中，各边与它所对的角的正弦之比相等. 即 (1.7) 利用正弦定理可以求解下列问题： （1）已知三角形的两个角和任意一边，求其他两边和一角. （2）已知三角形的两边和其中一边所对角，求其他两角和一边. 详细分析讲解 总结 归纳 详细分析讲解 思考 理解 记忆 理解 记忆 带领 学生 总结 20

您可能喜欢的文档

查看更多

热门课件教案

今日更新

在线
客服

相关
文档