搜PPT搜文档
当前位置：首页 > Word文档 > 教育教学 > 课件教案> 【高教版】中职数学拓展模块：1.3《正弦定理与余弦定理》教学设计

【高教版】中职数学拓展模块：1.3《正弦定理与余弦定理》教学设计

  • 页数：5页
  • 字数：约 2137 字
  • 大小：77.16KB
  • 格式：.docx
  • 版本：Office2016及以上版本
  • 作者：梁小A-PPT
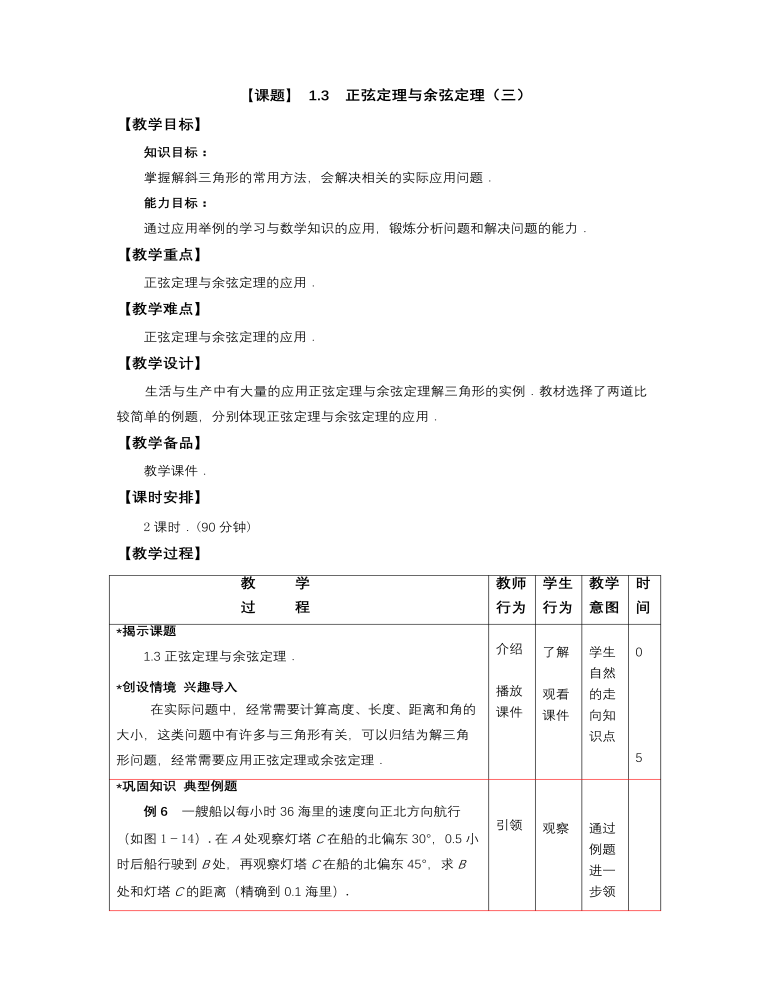
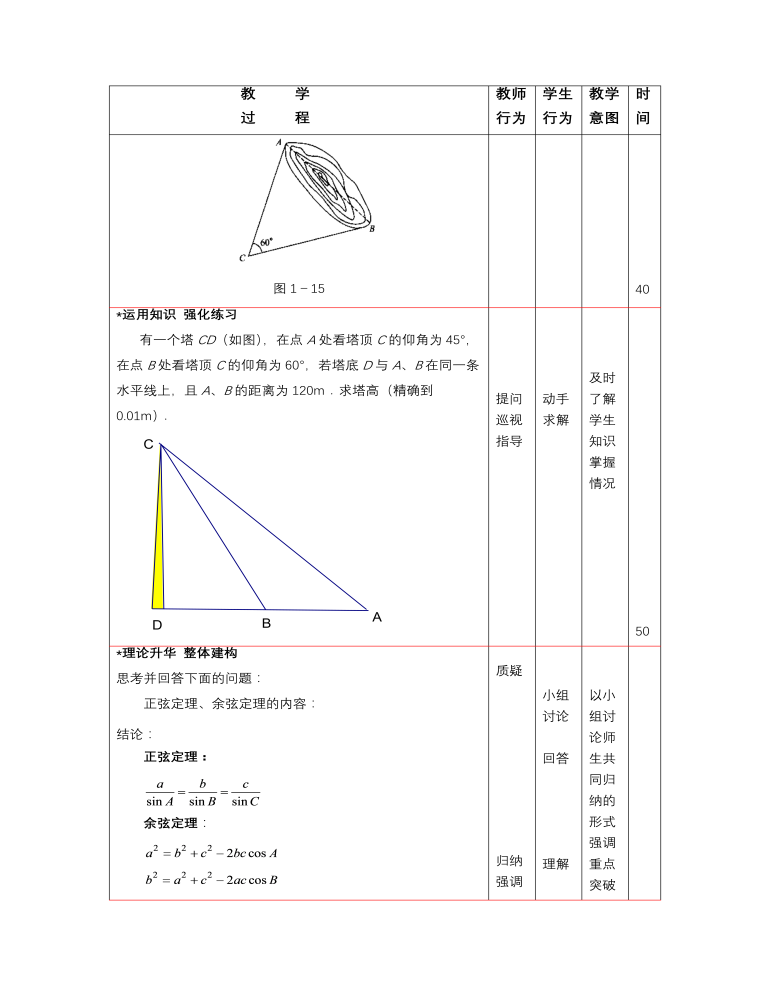
  • 【高教版】中职数学拓展模块：1.3《正弦定理与余弦定理》教学设计【高教版】中职数学拓展模块：1.3《正弦定理与余弦定理》教学设计【高教版】中职数学拓展模块：1.3《正弦定理与余弦定理》教学设计
  • 教 学 过 程教师 行为学生 行为教学 意图时间 *揭示课题 1.3正弦定理与余弦定理． *创设情境 兴趣导入 在实际问题中，经常需要计算高度、长度、距离和角的大小，这类问题中有许多与三角形有关，可以归结为解三角形问题，经常需要应用正弦定理或余弦定理． 介绍 播放 课件 了解 观看 课件 学生自然的走向知识点 0 5*巩固知识 典型例题 例6一艘船以每小时36海里的速度向正北方向航行（如图1－14）.在A处观察灯塔C在船的北偏东30°，0.5小时后船行驶到B处，再观察灯塔C在船的北偏东45°，求B处和灯塔C的距离（精确到0.1海里）. 解 因为∠NBC=45°，A=30°，所以C=15°， AB = 36×0.5 = 18 (海里). 由正弦定理得 答：B处离灯塔约为34.8海里. 例7 修筑道路需挖掘隧道，在山的两侧是隧道口A和B(图1－15），在平地上选择适合测量的点C，如果C=60°，AB = 350m，BC = 450m，试计算隧道AB的长度（精确到1m）． 解 在△ABC中，由余弦定理知 =167500． 所以AB≈409m. 答：隧道AB的长度约为409m. 图1－15 引领 讲解 说明 引领 观察 思考 主动 求解 观察 通过 例题 进一 步领 会 注意 观察 学生 是否 理解 知识 点 40

您可能喜欢的文档

查看更多

热门课件教案

今日更新

在线
客服

相关
文档