人教版新课标小学数学六年级上册圆教案
-
- 页数:19页
- 字数:约 9509 字
- 大小:121.50KB
- 格式:.doc
- 版本:Office2016及以上版本
- 作者:肖迪Ppter
圆教案
单元目标:
1、使学生认识圆,掌握圆的特征;理解直径与半径的相互关系;理解圆周率的意义,掌握圆周率的近似值。
2、使学生理解和掌握求圆的周长与面积的计算公式,并能正确地计算圆的周长与面积。
3、独立自学,使学生初步认识弧、圆心角和扇形。

4、使学生认识思对称图形,知道轴对称的含义,能找出轴对称图形的对称轴。
5、通过介绍圆周率的史料,使学生受到爱国主义教育。
单元重点:
1、认识圆和轴对称图形;
2、掌握圆的周长和面积的计算公式。
单元难点:
理解圆周率“π”;圆面积计算公式的推导以及画具有定半径或直径的圆。
1.认识圆
(1)圆的认识
教学目标:
1、使学生认识圆,掌握圆的特征,理解直径与半径的关系。
2、会使使用工具画圆。
3、培养学生观察、分析、综合、概括及动手操作能力。
教学重点:
圆的认识,通过动手操作,理解直径与半径的关系,认识圆的特征。
教学难点:画圆的方法,认识圆的特征。
教学过程:
一、复习。
1、我们以前学过的平面图行有哪些?这些图形都是用什么线围成的?简单说说这些图形的特征?
长方形 正方形 平行四边形 三角形 梯形
展示圆片图形:(1)圆是用什么线围成的?(圆是一种曲线图形)举例:生活中有哪些圆形
的物体?二、认识圆的特征。
1、学生自己在准备好的纸上画一个圆,并动手剪下。
2、动手折一折。
(1)折过2次后,你发现了什么?(两折痕的交点叫做圆心,圆心一般用字母O表示)
(2)再折出另外两条折痕,看看圆心是否相同。
3、认识直径和半径。
(1)将折痕用铅笔画出来,比一比是否相等?(2)观察这些线段的特征。(圆心和圆上任意一点的距离都相等)(3)板书:通过圆心并且两端都在圆上的线段,叫做直径。连接圆心到圆上任意一点的线段,叫做半径。
4、讨论:
(1)什么叫半径?圆上是什么意思?画一画两条半径,量一量它们的长短,发现了什么?
(2)什么叫直径?过圆心是什么意思?量一量手上的圆的直径的长短,你发现了什么?
(3)小结:在同一个圆里,有无数条直径,且所有的直径都相等。
在同一个圆里,有无数条半径,且所有的半径都相等。
5、直径与半径的关系。
(1)学生独立量出自己手中圆的直径与半径的长度,看它们之间有什么关系?然后讨论测量结果,找出直径与半径的关系。
得出结论:在同一个圆里d=2r
6、巩固练习:课本58“做一做”的第1-4题。
三、学习画圆。
1、介绍圆规的各部分名称及使用方法。
2、引导学生自学用圆规画圆,并小结出画圆的步骤和方法。
四、巩固练习。
1、画一个半径是2厘米的圆。再画一个直径是5厘米的圆。
2、判断,并说为什么。
(1)半径的长短决定圆的大小。( )
(2)圆心决定圆的位置。( )
(3)直径是半径的2倍。( )
(4)圆的半径都相等。( )
3、思考题:在操场如何画半径是5米的大圆?
五、布置作业。
书P60第1-4题。
(2)轴对称图形
教学目标:
1、在前面所学得成轴对称的平面图形的基础上,教学认识圆的对称轴。
2、使学生认识到圆是轴对称图形,且对称轴有无数条。
3、培养学生动手操作能力,在操作中加深对所学平面图形的对称轴的认识
教学重点:圆的对称轴。
教学难点:画对称轴的方法。
教学过程:
一、观察以前认识对称图形。
1、举例说出轴对称的物体。如:蝴蝶、飞机、门窗、圆中的钟面、月饼等。想一想这些图形有什么特点?
2、观察、概括。
如果一个图形沿着一条直线对折,两侧的图形能够完全重合,这个图形是轴对称图形。折痕所在的这条直线直线叫做对称轴。
二、教学认识圆的对称轴
1、出示例3:
你能分别画出下面两个圆的对称轴吗?你能画出几条?
2、学生尝试画出圆的对称轴,观察、再动手折一折,你发现了什么?
3、小结:圆有无数条对称轴。每一条直径所在的位置都是它的对称轴。
三、巩固练习。
1、在方格上画对称轴,并量出对称轴两边相对的点到对称轴的距离。
2、小结:对称轴两侧相对点到对称轴的距离相等。
3、从上面的图形可以看出,正方形、长方形、等腰三角形和圆都是轴对称图形,这些对称图形各有几条对称轴?画出来。
4、下面的图形是轴对称图形吗?它们各有几条对称轴?
长方形
等边三角形
等腰三角形
正方形
圆
环形
四、总结:
今天我们学习了哪些知识?
五、布置作业:
练习十四第5—9题。
教学追记:
本堂课是对圆的初步认识,概念较多,也能会较乏味。为了避免学生学得枯燥、没兴趣,我采用了课件与动手操作相结合的方式进行教学,充分调动起学生的学习积极性,并让学生在动手操作的基础上,自主探索和发现圆的有关特性。但在教学“画圆”时,我的讲授部分似乎就多了一些,如能让学生自己来讲述、演示画圆的步骤,有何不足在相互补充的话,这样的教学似乎会更好一些。
2、圆的周长和面积
(1)圆的周长
教学目标:
1、使学生理解圆的周长和圆周率的意义,理解并掌握圆的周长公式,并能
正确计算圆周长。
2、培养学生的观察、比较、概括和动手操作的能力。
3、对学生进行爱国主义教育。
教学重点:
圆的周长和圆周率的意义,圆周长公式的推导过程。
教学难点:
圆周长公式的推导过程。
教学过程:
一、认识圆的周长。
1、出示一个正方形。
这是什么图形?什么是正方形的周长?怎样计算?这个正方形周长与边长有什么关系?
C=4a
2、什么是圆的周长?
让学生上前比划,圆的周长在那?那一部分是圆的周长?
得出定义:围成圆的曲线的长叫做圆的周长。
二、圆周长的公式推导。
1、探索学习。
(1)你可以用什么办法知道一个圆的周长是多少?
(2)学生各抒己见,分别讨论说出自己的方法:
A、用一根线,绕圆一周,减去多余的部分,再拉直量出它的长度,即可得出圆的周长。
B、把圆放在直尺上滚动一周,直接量出圆的周长。
C、用一条小线的一端栓上小球在空中旋转。这样你能知道空中出现的圆的周长吗?
用滚动,绳测的方法可测量出圆的周长,但是有局限性。今天我们来探讨出一种求圆周长的普遍规律。
2、动手实践。
(1)4人小组,分别测量学具圆,报出自己量得的直径,周长,并计算周长和直径的比值。
(2)引生看表,问你们看周长与直径的比值有什么关系?
(3)你有办法验证圆的周长总是直径的3倍多一点吗?
(4)阅读课本P63,介绍圆周率,及介绍祖冲之。
3、解决新问题。
(1)教学例1
圆形花坛的直径是20m,它的周长是多少米?小自行车车轮的直径是50m,绕花坛一周车轮大约转动多少周?
第一个问题:
已知d=20米
求:C=?
根据C=πd
203.14=62.8(m)第二个问题:
已知:
小自行车d=50cm
先求小自行车C=?
c=πd 50cm=0.5m
0.53.14=1.57(m)再求绕花坛一周车轮大约转动多少周?
62.81.57=40(周)答:它的周长是62.8米。绕花坛一周车轮大约转动40周。
三、巩固练习。
1、求下列各题的周长。书本65页练习十五的第1题
2、判断正误。
(1)圆的周长是直径的3.14倍。( )
(2)在同圆或等圆中,圆的周长是半径的6.28倍。( )
(3)C=2πr=πd( )
(4)半圆的周长是圆周长的一半。( )
四、作业。
P64做一做,练习十五的第5、8题
圆的周长(2)教学目标:
1、通过教学使学生学会根据圆的周长求圆的直径、半径。
2、培养学生逻辑推理能力。
3、初步掌握变换和转化的方法。
教学重点:求圆的直径和半径。
教学难点:灵活运用公式求圆的直径和半径。
教学过程:
一、复习。
1、口答。
4π
2π
5π
10π
8π
2、求出下面各圆的周长。
C=πd
c=2πr
3.142
23.144
=6.28(厘米)=83.14
=25.12(厘米)二、新课。
1、提出研究的问题。
(1)你知道Π表示什么吗?
(2)下面公式的每个字母各表示什么?这两个公式又表示什么?
C=πd
C=2πr
(3)根据上两个公式,你能知道:
直径=周长圆周率
半径=周长(圆周率2)2、学习练习十四第2题。
(1)小红量得一个古代建筑中的大红圆柱的周长是3.768米,这个圆柱的直径是多少米?(得数保留一位小数)已知:c=3.77m
求:d=?
解:设直径是x米。
3.773.14
3.14x=3.77
x=3.773.14
x≈1.2米
(2)做一做。用一根1.2米长的铁条弯成一个圆形铁环,它的半径是多少?(得数保留两位小数)已知:c=1.2米
R=c(2Π)求:r=?
解:设半径为x米。
3.142x=1.2
1.223.14
6.28x=1.2=0.191
x=0.191≈0.19(米)x≈0.19
三、巩固练习。
1、饭店的大厅挂着一只大钟,这座钟的分针的尖端转动一周所走的路程是125.6厘米,它的分针长多少厘米?
2、求下面半圆的周长,选择正确的算式。
⑴3.148
⑵3.1482
⑶3.1482+8
3、一只挂钟分针长20cm,经过30分后,这根分针的尖端所走的路程是多少厘米?经过45分钟呢?
(1)想:钟面一圈是60分钟,走了30分,就是走了整个钟面的,也就是走了整个圆的。而钟面一圈的周长是多少?2023.14=125.6(厘米)
(2)想:钟面一圈是60分钟,走了45分,就是走了整个钟面的,也就是走了整个圆的。则:钟面一圈的周长是多少?
2023.14=125.6(厘米)45分钟走了多少厘米?
125.6=94.2(厘米)
4、P66第10题思考题。下图的周长是多少厘米?你是怎样计算的?
一、作业。P65-66二、第3、6、7、9题
教学追记:
圆的周长计算公式并不复杂,但这个公式如何得来,公式中的固定值“π”是如何来的,都是值得学生研究的问题。因次,教学中,我着力于培养学生的探究意识和探究能力,让学生利用实验的手段,通过测量、计算、猜测圆的周长和直径的关系、验证猜测等过程来理解并掌握圆的周长计算方法。因为是自己操作的所得,再加上我在课中介绍了一些相关资料及讲述了一个有趣的小故事,所以学生对“π”的含义就理解得特别透彻,也学得有兴趣。
圆的面积
教学内容:圆的面积第67-68页圆面积公式的推导。例1及做一做的第1题。练习十六的第1、2、5题。
教学目标:⒈使学生理解圆面积的含义,理解圆面积计算公式的推导过程,掌握圆面积的计算公式。
⒉培养学生动手操作、抽象概括的能力,运用所学知识解决简单实际问题。
⒊渗透转化的数学思想。
教学重点:圆面积的含义。圆面积的推导过程。
教学难点:圆面积的推导过程。
教学过程:
一、复习。
1、已知r,周长的一半怎样求?
2、用手中的三角板拼三角形,长方形、正方形、平行四边形等,并说出这些图形的面积计算公式。
s=ab
s=a2
s=
ah
s=ah
s=(a+b)h
二、新课。
1、什么是圆的面积?(出示纸片圆让生摸一摸)圆所占平面大小叫做圆的面积。
2、推导圆的面积公式。
(1)演示:将等分成16份的圆展开,问可拼成一个什么样的图形?
若分的分数越多,这个图形越接近长方形。
(1)找:找出拼出的图形与圆的周长和半径有什么关系?
圆的半径=长方形的宽
圆的周长的一半=长方形的长
长方形面积=长宽
所以:
圆的面积=圆的周长的一半圆的半径
S=πrr
S圆=πrr=πr2
3、你还能用其他方法推算出圆的面积公式吗?
(1)将圆16等份,取其中一份,看作是一个近似的三角形,三角形的面积是这个圆面积的。这个三角形底是圆周长的,三角形的高是圆的半径。
因为:三角形面积=底高
圆面积==rr=πr2
(2)将圆16等分,取其中两份,可以拼成一个近似的平行四边形。平行四边形面积是圆面积的 ,平行四边形的底是,三角形的高即一个半径,因为:平行四边形面积=底高
圆面积=r
= r8
=πr2
还可以取3份、4份等,同学们可以一一推算。
三、运用知识解决实际问题。
1、例1
一个圆的直径是20m,它的面积是多少平方米?
已知:d=20厘米
求:s=?
r=d2
202=10(m)s=Лr2
3.14102
=3.14100
=314(平方厘米)
2、根据下面所给的条件,求圆的面积。
r=5cm
d=0.8dm
3、解答下列各题。
(1)一个圆形茶几桌面的直径是1m,它的面积是多少平方厘米?
(2)公园草地上一个自动旋转喷灌装置的射程是10m。它能喷灌的面积是多少?
四、作业。
课本P70第1、5题。
圆的面积(2)
教学目标:
1、使学生学会已知圆的周长求圆的面积的解题思路与方法,理解并学会环形面积。
2、培养学生灵活、综合运用知识的能力,运用所学的知识解决简单的实际问题。
3、培养学生的逻辑思维能力。
教学重点:培养综合运用知识的能力。
教学难点:培养综合运用知识的能力。
教学过程:
一、复习。
1、口算:
32
42
52
82
92
202
2π
3π
6π
10π
7π
5π
2、思考:
(1)圆的周长和面积分别怎样计算?二者有何区别?
(2)求圆的面积需要知道什么条件?
(3)知道圆的周长能够求它的面积吗?
三、新课。
1、教学练习十六第3题
小刚量得一棵树干的周长是125.6cm,这棵树干的横截面积是多少?
已知:c=125.6厘米
s=πr2
r:125.6(23.14)3.14202
=125.66.28
=3.14400
=20(厘米)=1256(平方厘米)
答:这棵树干的横截面积1256平方厘米。
3、教学环形面积。
(1)例2
光盘的银色部分是个圆环,内圆半径是2cm,外圆半径是6cm。它的面积是多少?
已知:R=6厘米
r=2厘米
求:
s=?
3.1462
3.1422
=3.1436
=3.144
=113.04(平方厘米)=12.56(平方厘米)
113.04-12.56=100.48(平方厘米)
第二种解法:3.14(62-22)=100.48(平方厘米)
(2)小结:环形的面积计算公式:
S=πR2-πr2或S=π(R2-r2)
(3)完成做一做:
一个圆形环岛的直径是50m,中间是一个直径为10m的圆形花坛,其他地方是草坪。草坪的占地面积是多少?
收藏模板
会员免费下载
您可能喜欢的文档
查看更多
人教版新课标小学数学六年级上册总复习教案
- 页数:11页
- |大小:119.50KB
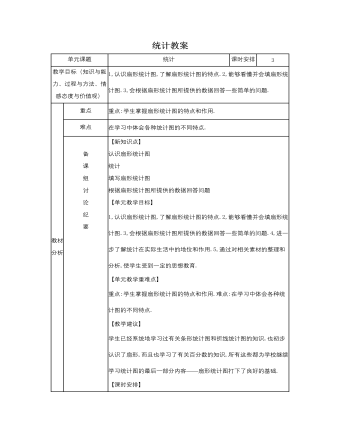
人教版新课标小学数学六年级上册统计教案
- 页数:5页
- |大小:121.00KB
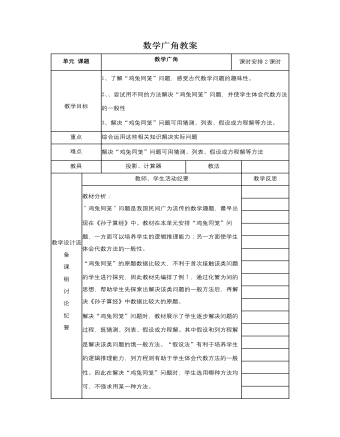
人教版新课标小学数学六年级上册数学广角教案
- 页数:8页
- |大小:202.00KB

人教版新课标小学数学六年级上册利息说课稿
- 页数:4页
- |大小:47.00KB

人教版新课标小学数学六年级上册折扣说课稿
- 页数:6页
- |大小:50.00KB

人教版新课标小学数学六年级上册百分数教案2篇
- 页数:35页
- |大小:397.00KB

人教版新课标小学数学六年级上册分数除法教案
- 页数:22页
- |大小:204.00KB
热门课件教案

部编版六年级语文上册《草原》教案
- 页数:6页
- |大小:265.86KB
- 课件教案

部编版语文八年级下册《社戏》教案
- 页数:8页
- |大小:340.00KB
- 课件教案

部编版语文八年级下册《时间的脚印》教案
- 页数:4页
- |大小:511.50KB
- 课件教案

《剪羊毛》教案
- 页数:3页
- |大小:33.50KB
- 课件教案

精选高中生期末评语
- 页数:42页
- |大小:7M
- 课件教案

部编版语文八年级下册《马说》教案
- 页数:8页
- |大小:367.50KB
- 课件教案
今日更新

精选高中生期末评语
- 页数:42页
- |大小:7M

××县招商局2024年上半年工作总结
- 页数:12页
- |大小:142.54KB

“四零”承诺服务创建工作总结
- 页数:5页
- |大小:39.83KB

“改作风、提效能”专项行动工作总结
- 页数:6页
- |大小:139.05KB

“大学习、大讨论、大调研”活动情况总结报告
- 页数:7页
- |大小:26.12KB

2024年度工作计划汇编(18篇)
- 页数:72页
- |大小:196.93KB






 微信支付
微信支付  支付宝支付
支付宝支付 