北师大版初中数学九年级下册频率与概率说课稿
-
- 页数:10页
- 字数:约 5480 字
- 大小:109.50KB
- 格式:.doc
- 版本:Office2016及以上版本
- 作者:二十四设计
频率与概率说课稿
各位专家、评委,上午好:
我是10号参赛选手,我说课的题目是《频率与概率》。我将从教材分析、教学策略、教学过程、教学反思,四个方面来具体阐述对本节教材的理解和教学设计。
一、教材分析:
1、地位与作用:《频率与概率》选自高等教育出版社出版,李广全、李尚志主编的中等职业教育课程改革国家规划新教材《数学》(基础模块)下册,第十章第二节的内容。本节课的最大特点是与人们的日常生活密切联系。而本节课的内容主要包括概率的定义和用频率估计概率的方法,安排1课时完成。本节课的学习,将为后面学习古典概型和用列举法求等可能性事件的概率打下基础,同时也为学生体会概率和统计之间的联系打下基础,在教材中处于非常重要的位置。

2、学情分析:本节课的授课对象是高二(2)班的会计专业的学生,女生偏多。学生数学基础较好。学生思维活跃,善于交流,动手操作能力强,对上节课的必然事件、随机事件、不可能事件知识已经理解并掌握,表现欲强。这些特点为本堂课的有效教学提供了质的保障。
3、教材内容处理和教学方式创新:1)用多重试验得出概率定义:对试验采用个人抛掷、对比结果、电脑模拟,让学生体验用试验方法获取知识形成的过程,体验数学求证的严谨性。2)课程内容与生活实际紧密相连:教学中将抛硬币、打靶、投篮、收视率等生活中的概率问题设计为教学情境、练习或例题,让数学变得有趣和富有吸引力。
4、教学目标:对于频率与概率这一节课的知识掌握并不难,但是学生积极的情感态度的培养、促进良好数学观的养成需要一个长期的过程,教材为学生提供了足够的探索和交流的空间,以利于改变学生的学习方式,体现了知识形成的过程。根据新课标的要求、教材内容及所任教班级学生学习的特点,我制定了如下的教学目标:
1)知识与技能目标:理解概率的含义并能通过大量重复试验确定概率。
2)过程与方法目标:以分组做试验的方式导入和展开课堂,通过分组讨论,合作交流的方式完成课堂学习。
3)情感目标:鼓励学生积极参与试验活动,主动与他人交流和合作,在活动中感受学习的乐趣。利用生活素材激发学生学习数学的热情和兴趣。通过分层设置问题培养学生学习数学的自信心。结合随机试验的随机性和规律性,让学生了解偶然性寓于必然性之中的辩证唯物主义思想。
5、教学重点、难点:
本节课主要是通过学生的动手试验发现知识、总结频率与概率之间的关系,根据教学目标以及对整个教材的理解。我认为课堂教学不仅应把数学知识作为教学重点,而且能力的培养也应作为重点,所以我确定本节课的
教学重点:通过实验让学生理解当试验次数较大时,试验频率稳定于理论概率,并据此能估计出某一事件发生的概率。
教学难点:正确理解频率和概率的关系,以及理解每次试验结果的随机性与大量随机试验结果的规律性。
二、教学策略
通过以上分析,为了达到较好的教学效果,本课首先采用以启发为主,分层次设置问题,加入适量的情景设置,运用实验探究展开课堂;接着对问题采用多种展示手法,以学生为主体,让学生分组讨论,合作学习,探究学习。
我所采用的教学方法有情境教学法、实验教学法、讲练教学法。
在上课之前我做了如下准备
(1)分组:
(2)每人准备1枚1元硬币
(3)实验登记表
三、教学过程
整个教学过程分为5个环节:①。。②。。③。。。。。
各环节时间安排如下:
(一)创设情境,引入课题:
问题1:抛硬币对比赛公平吗?
师:如果让两个同学举行象棋比赛,如何公平决定让谁先走棋呢?
学生答案预测:甲:用剪刀石头布决定。
乙:抓阄
丙:抛硬币
师:抛掷硬币对比赛双方公平吗?为什么?
学生可能会回答公平,但为什么公平学生可能回答不上来。
(这时学生会心存疑问,为了弄清事实,主动参与到课堂中来,表现出急切地破解心中疑团的愿望。)
(设计意图:以具体情境为背景,让学生都参与到教学活动中来,吸引学生的注意力,调动学生学习的积极性。从学生熟悉的问题入手,引发学生深层思考,使学生产生强烈的求知欲望)
师:究竟公不公平呢?如果不公平,正面向上的可能性是多少?反面向上的可能性又是多少?
由此引导学生进入第二环节:
(二)试验探究
本环节分为六部分:第一部分分组试验,要求每个学生抛掷硬币10次,并做好记录,统计出正面向上的次数和反面向上的次数,填入表格1.
然后各小组长,汇总本组6名成员的数据填入表格2,
最后全班共同完成表格3
1、分组试验
全班共分8个小组,每小组7人(其中挑选一人为组长),每人抛10次,共480次。组长不参与抛掷。
(1)抛掷要求:①两人一组合,完成10次抛掷,一个人抛,一个人记录。正面向上记为“1”,反面向上记为“0”,10次完成后统计正面向上和反面向上的总数;②抛的高度要达到自己坐姿的头顶高度。
(2)组长职责:①检查组员抛掷是否符合要求;②收集本组数据,把数据录入教师机中的抛掷情况表。全班共同填写硬币抛掷统计表(表3),将第1组数据填在第一列,第1、2组的数据之和填在第二列,……8个组的数据之和填在第8列。
(设计意图:①“在相同条件下”使数据更真实有效;②合理分组,加快试验速度,既培养动手能力与探索精神,又培养团队协作精神。)
表1(每人抛掷情况统计表)
姓名
抛掷硬币情况记录表
次数
1
2
3
4
5
6
7
8
9
10
正面向上次数
反面向上次数
结果
表2(各小组抛掷情况汇总表)
小组
一
二
三
四
五
六
七
八
正面向上的频数m1
反面向上的频数m2
正面向上的频率
反面向上的频率
表3(硬币抛掷统计表)
抛掷次数n
60
120
180
240
300
360
420
480
正面向上的频数m1
反面向上的频数m2
正面向上的频率
反面向上的频率
2、分析试验结果
(第2部分分析结果:针对表2,表3,设置了2个问题让小组讨论)
提问(1):观察表2,各小组正面朝上的频率一样吗?各小组反面朝上的频率一样吗?
提问(2):从表3的规律可知,抛掷次数更大时,正面朝上的频率估计是多少?
(以此引导认识随机事件的发生具有偶然性;当次数逐渐增大的情况下,正面向上的频率数值渐趋稳定。)
(设计意图:通过提问1:引导学生认识到随机事件的发生具有偶然性。提问2:引导学生发现在次数逐渐增大的情况下,频率数值渐趋稳定。)
3、比较试验
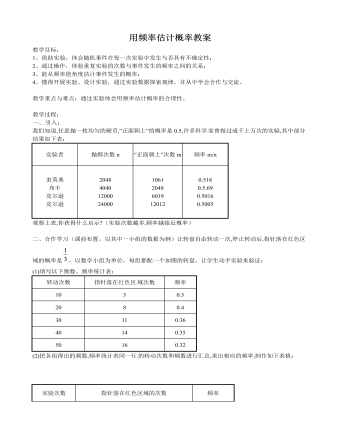
由此我们可以得到,随着抛掷次数的不断增加,频率越来越集中在0.5的附近。历史上,还有些数学家做了成千上万次掷硬币的实验,结果如下表:
实验者
抛掷次数(n)
正面向上的次数(m)
正面向上的频率(m/n)
蒲 丰
4040
2048
0.5069
皮尔逊
12000
6019
0.5016
皮尔逊
24000
12012
0.5005
维尼
30000
14994
0.4998
(设计意图:让学生对历史上的数学家们所做的实验和自己分组所做的实验进行对比得出:几位数学家的试验结果跟自己的试验结果大致相同,大量试验次数下频率数值稳定于0.5。这样学生会很有成就感,老师趁此提出鼓励和希望,只要努力你们也可以成为数学家。)
4、电脑模拟实验
利用电脑模拟实验,让学生在计算机中输入实验次数,然后观察得到的结果,并和自己之前的实验数据,科学家的数据相对比,了解电脑的模拟功能。最后指导学生进行实验总结:
(试验次数越大,正面向上与反面向上的频率都稳定于0.5。因此两者发生的可能性相等,从而验证了“公平”的猜想。)
(三)揭示新知
问题2:我们能否用频率估计概率呢?
师:其实,不仅仅是掷硬币有规律,人们在大量的生产生活中发现:对于一般的随机事件,在做大量重复试验时,随着试验次数的增加,一个事件出现的频率也总在一个固定数附近摆动,显示出一定的稳定性。
频率的稳定性揭示出随机事件发生的可能性有一定大小。
(通过以上试验,学生会明白:事件的频率稳定在某一数值附近,我们就可用这一数值表示事件发生的可能性的大小。由此带出概率的定义:)
给出定义:
一般地,在n次重复进行的试验中,事件A发生的频率,当n很大时,总是在某个常数附近摆动,随着n的增加,摆度幅度越来越小,这时就把这个常数叫作事件A的概率,记为P(A)。
问题3:随机事件的概率P(A)有什么范围?对一个随机事件A,用频率估计的概率P(A)可能小于0吗?可能大于1吗?
因为在n次重复试验中,事件A发生的次数m总是满足,所以,因此得到事件的概率具有以下性质:
(1)必然事件的概率为1,
(2)不可能事件的概率为0;
(3)
(接着:为了更好地理解概率的定义,指导学生分析频率 m/n 的取值范围,并得出概率的性质;另外通过分析概率的定义,让学生明白频率与概率的关系:概率是频率的稳定值,而频率是概率的近似值)
(设计意图:通过分析取值范围,学生对概率的定义以及用频率估计概率的内涵有更深一层的认识。)
(三)知识应用加深理解
例1
让学生填写频率和估计概率:
连续抽检了某车间一周内的产品,结果如表10-2所示(精确到0.001)
表10-2
星期
星期一
星期二
星期三
星期四
星期五
星期六
星期日
生产产品总数n
60
150
600
900
1200
1800
2400
次品数m
7
19
52
100
109
169
248
频率
0.117
0.127
0.087
0.111
0.094
0.103
问题(1)计算星期五次品的频率是多少?
(2)估计该厂生产的次品的概率是多少?
(设计意图:通过本题,让学生更具体的理解概率,巩固概率和频率的关系,了解频率不一定等于概率,而是围绕概率波动。同时也让学生进一步认识到,大量重复实验是确定概率的一种方法。)
例2 在有一个10万人的小镇,随机调查了2000人,其中有250人看中央电视台的早间新闻.在该镇随便问一个人,他看早间新闻的概率大约是多少?该镇看中央电视台早间新闻的大约是多少人?
解:根据概率的意义,可以认为其概率大约等于250/2000=0.125.
该镇约有1000000.125=12500人看中央电视台的早间新闻.
(例题2是通过概率的计算,反过来估计节目收看的人数)
(四)巩固知识适当拓展:
1、某篮球运动员在同一条件下进行投篮练习,结果如下表:
投篮次数
8
10
15
20
30
40
50
命中次数
6
8
12
17
25
32
39
命中率
(1)计算表中进球的频率;
(2)这位运动员投篮一次,进球的概率约是多少?
您可能喜欢的文档
查看更多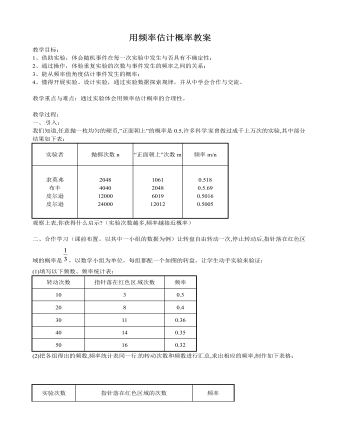
北师大初中数学九年级上册用频率估计概率2教案
- 页数:3页
- |大小:224.50KB

北师大初中数学九年级上册用频率估计概率1教案
- 页数:3页
- |大小:256.00KB

北师大初中数学九年级上册用频率估计概率1教案
- 页数:3页
- |大小:256.00KB
北师大初中数学九年级上册用频率估计概率2教案
- 页数:3页
- |大小:224.50KB

北师大初中七年级数学下册频率的稳定性教案
- 页数:4页
- |大小:1M
北师大初中数学九年级上册概率与游戏的综合运用2教案
- 页数:2页
- |大小:213.00KB

北师大初中数学九年级上册用树状图或表格求概率1教案
- 页数:3页
- |大小:280.50KB
热门说课稿

雾在哪里说课稿
- 页数:3页
- |大小:46.00KB
- 说课稿

幼儿园中班课后说课稿 雪花和雨滴
- 页数:3页
- |大小:37.00KB
- 说课稿

《陀螺》说课稿
- 页数:4页
- |大小:39.00KB
- 说课稿

高中历史人教版必修一《第22课祖国统一大业》说课稿
- 页数:3页
- |大小:46.07KB
- 说课稿

小学数学人教版一年级上册《认识钟表》说课稿
- 页数:4页
- |大小:24.27KB
- 说课稿

小学数学人教版三年级下册《0的除法》说课稿
- 页数:6页
- |大小:34.92KB
- 说课稿
今日更新

精选高中生期末评语
- 页数:42页
- |大小:7M

××县招商局2024年上半年工作总结
- 页数:12页
- |大小:142.54KB

“四零”承诺服务创建工作总结
- 页数:5页
- |大小:39.83KB

“改作风、提效能”专项行动工作总结
- 页数:6页
- |大小:139.05KB

“大学习、大讨论、大调研”活动情况总结报告
- 页数:7页
- |大小:26.12KB

2024年度工作计划汇编(18篇)
- 页数:72页
- |大小:196.93KB





