热门搜索
小班主题活动探究课件教案文档

人教A版高中数学必修一正弦函数、余弦函数的性质教学设计(2)
本节课是正弦函数、余弦函数图像的继续,本课是正弦曲线、余弦曲线这两种曲线的特点得出正弦函数、余弦函数的性质. 课程目标1.了解周期函数与最小正周期的意义;2.了解三角函数的周期性和奇偶性;3.会利用周期性定义和诱导公式求简单三角函数的周期;4.借助图象直观理解正、余弦函数在[0,2π]上的性质(单调性、最值、图象与x轴的交点等);5.能利用性质解决一些简单问题. 数学学科素养1.数学抽象:理解周期函数、周期、最小正周期等的含义; 2.逻辑推理: 求正弦、余弦形函数的单调区间;3.数学运算:利用性质求周期、比较大小、最值、值域及判断奇偶性.4.数学建模:让学生借助数形结合的思想,通过图像探究正、余弦函数的性质.重点:通过正弦曲线、余弦曲线这两种曲线探究正弦函数、余弦函数的性质; 难点:应用正、余弦函数的性质来求含有cosx,sinx的函数的单调性、最值、值域及对称性.
- 下载

人教A版高中数学必修一指数函数的概念教学设计(2)
指数函数与幂函数是相通的,本节在已经学习幂函数的基础上通过实例总结归纳指数函数的概念,通过函数的三个特征解决一些与函数概念有关的问题.课程目标1、通过实际问题了解指数函数的实际背景;2、理解指数函数的概念和意义.数学学科素养1.数学抽象:指数函数的概念;2.逻辑推理:用待定系数法求函数解析式及解析值;3.数学运算:利用指数函数的概念求参数;4.数学建模:通过由抽象到具体,由具体到一般的思想总结指数函数概念.重点:理解指数函数的概念和意义;难点:理解指数函数的概念.教学方法:以学生为主体,采用诱思探究式教学,精讲多练。教学工具:多媒体。一、 情景导入在本章的开头,问题(1)中时间 与GDP值中的 ,请问这两个函数有什么共同特征.要求:让学生自由发言,教师不做判断。而是引导学生进一步观察.研探.
- 下载
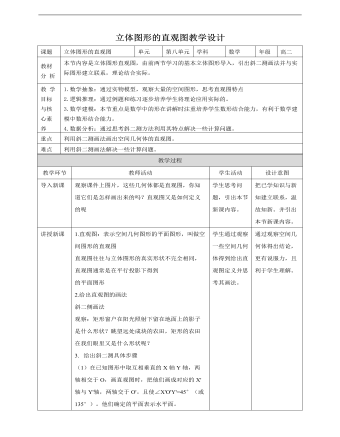
人教A版高中数学必修二立体图形直观图教学设计
1.直观图:表示空间几何图形的平面图形,叫做空间图形的直观图直观图往往与立体图形的真实形状不完全相同,直观图通常是在平行投影下得到的平面图形2.给出直观图的画法斜二侧画法观察:矩形窗户在阳光照射下留在地面上的影子是什么形状?眺望远处成块的农田,矩形的农田在我们眼里又是什么形状呢?3. 给出斜二测具体步骤(1)在已知图形中取互相垂直的X轴Y轴,两轴相交于O,画直观图时,把他们画成对应的X'轴与Y'轴,两轴交于O'。且使∠X'O'Y'=45°(或135°)。他们确定的平面表示水平面。(2)已知图形中平行于X轴或y轴的线段,在直观图中分别画成平行于X'轴或y'轴的线段。(3)已知图形中平行于X轴的线段,在直观图中保持原长度不变,平行于Y轴的线段,在直观图中长度为原来一半。4.对斜二测方法进行举例:对于平面多边形,我们常用斜二测画法画出他们的直观图。如图 A'B'C'D'就是利用斜二测画出的水平放置的正方形ABCD的直观图。其中横向线段A'B'=AB,C'D'=CD;纵向线段A'D'=1/2AD,B'C'=1/2BC;∠D'A'B'=45°,这与我们的直观观察是一致的。5.例一:用斜二测画法画水平放置的六边形的直观图(1)在六边形ABCDEF中,取AD所在直线为X轴,对称轴MN所在直线为Y轴,两轴交于O',使∠X'oy'=45°(2)以o'为中心,在X'上取A'D'=AD,在y'轴上取M'N'=½MN。以点N为中心,画B'C'平行于X'轴,并且等于BC;再以M'为中心,画E'F'平行于X‘轴并且等于EF。 (3)连接A'B',C'D',E'F',F'A',并擦去辅助线x轴y轴,便获得正六边形ABCDEF水平放置的直观图A'B'C'D'E'F' 6. 平面图形的斜二测画法(1)建两个坐标系,注意斜坐标系夹角为45°或135°;(2)与坐标轴平行或重合的线段保持平行或重合;(3)水平线段等长,竖直线段减半;(4)整理.简言之:“横不变,竖减半,平行、重合不改变。”
- 下载
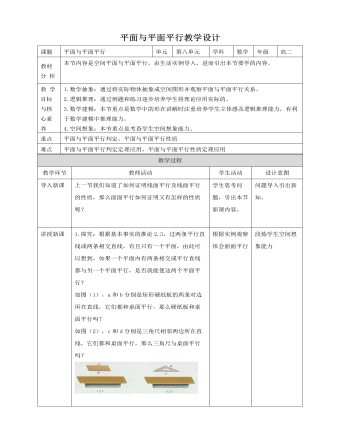
人教A版高中数学必修二平面与平面平行教学设计
1.探究:根据基本事实的推论2,3,过两条平行直线或两条相交直线,有且只有一个平面,由此可以想到,如果一个平面内有两条相交或平行直线都与另一个平面平行,是否就能使这两个平面平行?如图(1),a和b分别是矩形硬纸板的两条对边所在直线,它们都和桌面平行,那么硬纸板和桌面平行吗?如图(2),c和d分别是三角尺相邻两边所在直线,它们都和桌面平行,那么三角尺与桌面平行吗?2.如果一个平面内有两条平行直线与另一个平面平行,这两个平面不一定平行。我们借助长方体模型来说明。如图,在平面A’ADD’内画一条与AA’平行的直线EF,显然AA’与EF都平行于平面DD’CC’,但这两条平行直线所在平面AA’DD’与平面DD’CC’相交。3.如果一个平面内有两条相交直线与另一个平面平行,这两个平面是平行的,如图,平面ABCD内两条相交直线A’C’,B’D’平行。
- 下载
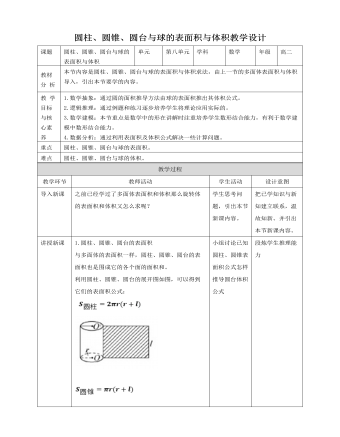
人教A版高中数学必修二圆柱、圆锥、圆台和球的表面积与体积教学设计
1.圆柱、圆锥、圆台的表面积与多面体的表面积一样,圆柱、圆锥、圆台的表面积也是围成它的各个面的面积和。利用圆柱、圆锥、圆台的展开图如图,可以得到它们的表面积公式:2.思考1:圆柱、圆锥、圆台的表面积之间有什么关系?你能用圆柱、圆锥、圆台的结构特征来解释这种关系吗?3.练习一圆柱的一个底面积是S,侧面展开图是一个正方体,那么这个圆柱的侧面积是( )A 4πS B 2πS C πS D 4.练习二:如图所示,在边长为4的正三角形ABC中,E,F分别是AB,AC的中点,D为BC的中点,H,G分别是BD,CD的中点,若将正三角形ABC绕AD旋转180°,求阴影部分形成的几何体的表面积.5. 圆柱、圆锥、圆台的体积对于柱体、锥体、台体的体积公式的认识(1)等底、等高的两个柱体的体积相同.(2)等底、等高的圆锥和圆柱的体积之间的关系可以通过实验得出,等底、等高的圆柱的体积是圆锥的体积的3倍.
- 下载
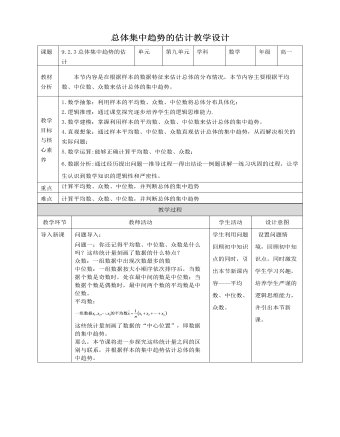
人教A版高中数学必修二总体集中趋势的估计教学设计
(2)平均数受数据中的极端值(2个95)影响较大,使平均数在估计总体时可靠性降低,10天的用水量有8天都在平均值以下。故用中位数来估计每天的用水量更合适。1、样本的数字特征:众数、中位数和平均数;2、用样本频率分布直方图估计样本的众数、中位数、平均数。(1)众数规定为频率分布直方图中最高矩形下端的中点;(2)中位数两边的直方图的面积相等;(3)频率分布直方图中每个小矩形的面积与小矩形底边中点的横坐标之积相加,就是样本数据的估值平均数。学生回顾本节课知识点,教师补充。 让学生掌握本节课知识点,并能够灵活运用。
- 下载
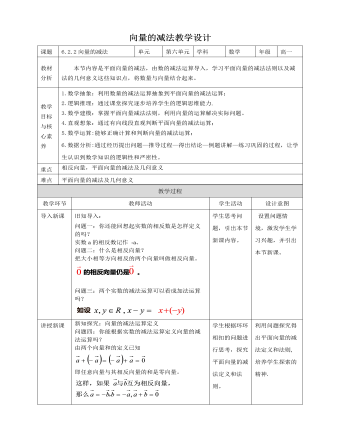
人教A版高中数学必修二向量的减法运算教学设计
新知探究:向量的减法运算定义问题四:你能根据实数的减法运算定义向量的减法运算吗?由两个向量和的定义已知 即任意向量与其相反向量的和是零向量。求两个向量差的运算叫做向量的减法。我们看到,向量的减法可以转化为向量的加法来进行:减去一个向量相当于加上这个向量的相反向量。即新知探究(二):向量减法的作图方法知识探究(三):向量减法的几何意义问题六:根据问题五,思考一下向量减法的几何意义是什么?问题七:非零共线向量怎样做减法运算? 问题八:非零共线向量怎样做减法运算?1.共线同向2.共线反向小试牛刀判一判(正确的打“√”,错误的打“×”)(1)两个向量的差仍是一个向量。 (√ )(2)向量的减法实质上是向量的加法的逆运算. ( √ )(3)向量a与向量b的差与向量b与向量a的差互为相反向量。 ( √ )(4)相反向量是共线向量。 ( √ )
- 下载

人教A版高中数学必修二直线与平面垂直教学设计
1.观察(1)如图,在阳光下观察直立于地面的旗杆AB及它在地面影子BC,旗杆所在直线与影子所在直线的位置关系是什么?(2)随着时间的变化,影子BC的位置在不断的变化,旗杆所在直线AB与其影子B’C’所在直线是否保持垂直?经观察我们知道AB与BC永远垂直,也就是AB垂直于地面上所有过点B的直线。而不过点B的直线在地面内总是能找到过点B的直线与之平行。因此AB与地面上所有直线均垂直。一般地,如果一条直线与一个平面α内所有直线均垂直,我们就说l垂直α,记作l⊥α。2.定义:①文字叙述:如果直线l与平面α内的所有 直线都垂直,就说直线l与平面α互相垂直,记作l⊥α.直线l叫做平面α的垂线,平面α叫做直线l的垂面.直线与平面垂直时,它们唯一的公共点P叫做交点.②图形语言:如图.画直线l与平面α垂直时,通常把直线画成与表示平面的平行四边形的一边垂直.③符号语言:任意a?α,都有l⊥a?l⊥α.
- 下载
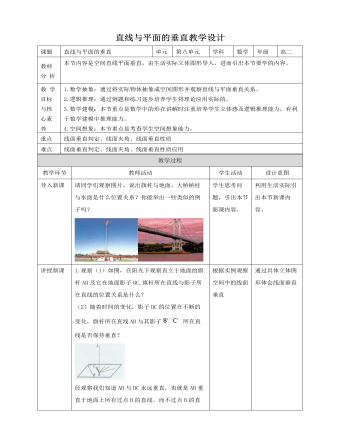
人教A版高中数学必修二直线与平面垂直教学设计
1.观察(1)如图,在阳光下观察直立于地面的旗杆AB及它在地面影子BC,旗杆所在直线与影子所在直线的位置关系是什么?(2)随着时间的变化,影子BC的位置在不断的变化,旗杆所在直线AB与其影子B’C’所在直线是否保持垂直?经观察我们知道AB与BC永远垂直,也就是AB垂直于地面上所有过点B的直线。而不过点B的直线在地面内总是能找到过点B的直线与之平行。因此AB与地面上所有直线均垂直。一般地,如果一条直线与一个平面α内所有直线均垂直,我们就说l垂直α,记作l⊥α。2.定义:①文字叙述:如果直线l与平面α内的所有 直线都垂直,就说直线l与平面α互相垂直,记作l⊥α.直线l叫做平面α的垂线,平面α叫做直线l的垂面.直线与平面垂直时,它们唯一的公共点P叫做交点.②图形语言:如图.画直线l与平面α垂直时,通常把直线画成与表示平面的平行四边形的一边垂直.
- 下载
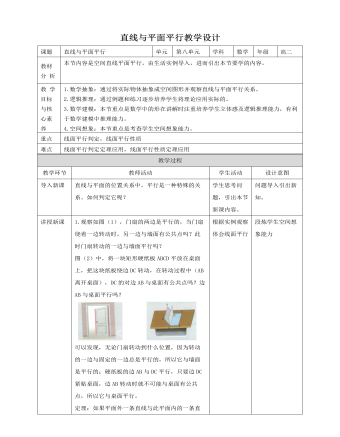
人教A版高中数学必修二直线与直线垂直教学设计
6.例二:如图在正方体ABCD-A’B’C’D’中,O’为底面A’B’C’D’的中心,求证:AO’⊥BD 证明:如图,连接B’D’,∵ABCD-A’B’C’D’是正方体∴BB’//DD’,BB’=DD’∴四边形BB’DD’是平行四边形∴B’D’//BD∴直线AO’与B’D’所成角即为直线AO’与BD所成角连接AB’,AD’易证AB’=AD’又O’为底面A’B’C’D’的中心∴O’为B’D’的中点∴AO’⊥B’D’,AO’⊥BD7.例三如图所示,四面体A-BCD中,E,F分别是AB,CD的中点.若BD,AC所成的角为60°,且BD=AC=2.求EF的长度.解:取BC中点O,连接OE,OF,如图。∵E,F分别是AB,CD的中点,∴OE//AC且OE=1/2AC,OF//AC且OF=1/2BD,∴OE与OF所成的锐角就是AC与BD所成的角∵BD,AC所成角为60°,∴∠EOF=60°或120°∵BD=AC=2,∴OE=OF=1当∠EOF=60°时,EF=OE=OF=1,当∠EOF=120°时,取EF的中点M,连接OM,则OM⊥EF,且∠EOM=60°∴EM= ,∴EF=2EM=
- 下载

人教部编版道德与法制五年级上册美丽文字,民族瑰宝
学生阅读欣赏教材第66页王羲之的《兰亭集序》和柳公权的《玄秘塔碑》,然后,教师引导学生说说自己喜欢的字体,并将课前搜集到的字帖或者自己的书法作品与同学分享。设计意图:引导学生欣赏汉字的书法艺术,体验书法的艺术美。环节三:课堂小结,内化提升学生谈一谈学习本节课的收获,教师相机引导。设计意图:梳理总结,体验收获与成功的喜悦,内化提升学生的认识与情感。环节四:布置作业,课外延伸课后,以古老而优美的汉字为主题办一期手抄报。设计意图:将课堂所学延伸到学生的日常生活中,有利于落实行为实践。六、板书设计为了突出重点,让学生整体上感知本节课的主要内容,我将以思维导图的形式设计板书:在黑板中上方的中间位置是课题《美丽文字,民族瑰宝》,下面是:直观形象,生动多姿;形体优美,风格迥异。
- 下载

全市纪检监察干部队伍教育整顿暨年度干部监督工作总结
深入进行集体反思。主动检讨反思张某严重违纪违法案件暴露出的责任履行不到位、理想信念教育缺失等突出问题,进一步强化纪法意识,压实政治责任。召开了专题民主生活会,领导班子带头反思、带头自省,对案例谈认识体会,并结合自身和分管工作实际,围绕理想信念、责任落实、制度执行、队伍建设等方面对照检视,认真开展批评与自我批评,查摆问题和不足27个,深刻分析问题成因,提出下步努力方向和切实可行的整改措施43条,以“关键少数”反思整改的成效带动全系统对照整治。扎实开展警示教育。以张某严重违纪违法案件为镜鉴,召开全市纪检监察系统警示教育大会,向全系统通报案件教训警示情况,主要领导对加强队伍建设和廉政教育工作提出要求,教育引导干部引以为戒、警钟长鸣,筑牢拒腐防变思想防线。分析纪检监察干部在监督执纪执法和日常政务工作中可能存在的廉洁风险点,制定《全市纪检监察干部廉洁履职承诺书》,在警示教育大会上组织全体纪检监察干部签订《承诺书》152份,立下严守纪律、忠诚履职“军令状”,从严淬炼、重塑铁军队伍。
- 下载

巩固和深化ZT教育成果凝聚高质量发展强大力量工作总结
巩固深化ZT教育成果,进一步凝聚推动贵阳高质量发展的强大力量,要求我们坚持不懈在学懂弄通做实新时代中国特色社会主义思想中涵养初心、引领使命,切实做到学思用贯通、知信行统一。要坚持以人民为中心的发展思想,自觉同人民群众想在一起、干在一起,以看得见的变化回应群众期盼。要发扬斗争精神,加强实践锻炼、坚持实干导向,勇于担当作为;要敢于直面问题,勇于自我革命,把全市各级D组织锻造得更加坚强有力。要坚持把“当下改”与“长久立”结合起来,把建章立制和解决问题统一起来,不断巩固深化我市ZT教育成果。守初心、担使命永远在路上。让我们更加紧密地团结在以同志为核心的D中央周围,牢记嘱托守初心、感恩奋进担使命,切实做到一个D员就是一面旗帜,一个支部就是一座堡垒,以坚定不移的决心、坚如磐石的信心、坚持不懈的恒心,坚决打好全面建成小康社会和“十三五”规划收官之战,奋力开创贵阳更加美好的未来。
- 下载

纪检监察干部队伍教育整顿总结用经典句子70条
57、创新形式载体,采取现场教学、专题辅导、案例分析、交流研讨等多种形式,推动“第一议题”学习走深走实。58、围绕“书中凝心聚魂,学以淬火砺剑”主题,组织年轻干部开展读书分享活动,用书香滋养浩然气、以学习坚定报国志。59、聚焦“回头看”发现的问题短板,及时查漏补缺、推动整改,巩固深化学习教育成效。60、围绕“动力足不足、内容全不全、方式活不活、体悟深不深、用得好不好”逐条逐项对照检查,制定问题清单,认真对照自查。61、有思想上的“破冰”才会有行动上的“突围”。62、集中开展培训,提升思想认识;制定学习计划,明确学习重点;丰富学习活动,营造学习氛围;深入整治整改,推动履职尽责。63、强化政治建设;聚焦顽瘴痼疾;健全长效机制。
- 下载

2024年第一批ZT教育工作总结(自查报告)及下一步工作思路
一是理论学习还存在不少的差距。部分单位领导班子集中学习、交流研讨等抓得比较紧,但基层D支部和普通D员尤其是生产一线、流动D员参与性不高,不同程度存在温差落差现象。二是调查研究成果转化不佳。少数单位对规定要求研究不深、结合不紧、落实不够,甚至还存在赶进度、“转段”的思想。三是为民务实的导向还不够鲜明。个别单位在涉及民生、群众关注度高的问题上整改力度不大,效果不理想,与群众的期盼有差距。四是统筹联动合力还不够强。有的单位就ZT教育抓ZT教育,缺乏统筹意识、全局思维,存在学做“两张皮”现象,等等。对这些问题,我们将采取有效措施,切实加以解决。三、推动ZT教育走深走实的下步工作思路下一步,全省ZT教育将按照关于ZT教育的一系列重要指示精神和x、x委的部署要求,更大力度推进落实x重点措施,学习教育上持续深化,特别是要把新时代爱国主义教育作为学习教育的重要内容;调查研究上务求实效,重点抓好调研成果转化,做好调研的“后半篇文章”,在深入调研的基础上讲好专题D课;检视问题上深刻剖析,开好专题民主生活会;整改落实上动真碰硬,更大力度解决实际问题,不断推动ZT教育走深走实。
- 下载

教师在XX中学暑期师德师风专项巡查和整治工作总结
学校还设立举报箱公布举报热线暑期安排值班人员及时收集有关教师师德师风情况的反馈息。从多角度、多渠道强化师德师风建设每位教师都受社会和人民的监督。五、严格查处有偿家教根据教育局规定严禁教师从事有偿家教。除了会议上多次强调以外我校教师还签订“关于拒有偿家教”的承诺书。同时师德师风专项巡查和整治领导小组利用暑假期间不定期深入群众中去通过走访调查、实地考察等途径实时掌握我校教师是否存在“有偿家教”的问题一经发现及时制止并汇报教育局。至今止我校并未发现有师从事有偿补课的现象。总之通过狠抓师德师风建设工作使学校教师深深体会到只有制度完善、强过程管理发现问题及时处理才能证师德建设有成效。这次暑期师德师风专项巡查和整治以法制学习教育和组织教师进行自查依托以“以法治校”的制度管理、科学评估、重在激励手段形成良好的教师队伍树立教师的职业道德形象。
- 下载

关于纪检监察干部队伍教育整顿“回头看”总结报告
二、存在的问题一是教育整顿与主题教育结合度不够,部分书籍配备不全;二是警示教育开展较少;三是个人学习笔记存在机械式抄原文,将学习内容联系到工作和个人实际不够,心得体会太少;四是局限于对书本学习,组织纪检监察干部开展交流研讨少。三、下步工作计划(一)聚焦任务,再过一遍“细筛子”。对集中学习、问题查摆、整改落实、建章立制等重点任务全面督导检查,及时对发现各类问题形成清单、现场交办、限时整改。(二)直面问题,再下一次“硬功夫”。组织纪检监察干部主动认领问题、主动担当责任,逐一研判分析,细化整改措施,层层传导压力,自觉抓好整改落实。(三)建章立制,再建一道“防火墙”。坚持着眼长远、立足当前,分析存在问题,听取意见建议,对接形势政策,研究完善长效制度,织密履行监督、工作规范运行的“防火墙”。
- 下载

2024年市教育局在上半年工作总结和下半年工作谋划
(三)不断筑牢安全防线。一是守牢纪律作风、师德师风底线。继续开展“师德先进个人、集体”评选活动,进一步健全宣传、教育、考核、奖惩、监督“五位一体”的师德建设长效机制。二是守牢校园安全底线。全面加强校园“三防”建设,常态化开展校园及周边综合治理、消防安全、交通安全、房屋安全、汛期防汛防风防暴雨等工作。三是守牢身心健康底线。组织校医、健康副校长开展健康知识专题讲座;进一步健全食品安全管理制度;持续做好教师心理学培训;持续完善“同心圆心灵之家”网络平台,积极推进XX市心理健康教育示范校建设。(四)全面提升教育质量。一是强化素质教育。推进思政大中小学校一体化建设,进一步强化家庭教育和学校教育融合;做好2024年高三学业水平体育考试工作;迎接XX市教育局对美育示范校的评估验收。二是强化基础教育。
- 下载

XX县纪委监委开展纪检监察干部队伍教育整顿阶段总结报告
二、存在主要问题和不足一是落实学习教育计划有偏差。尽管我们制定了学习教育的计划,也明确了“六学联动”机制内容,但是与我们原计划4月上旬落实完毕有很大的距离。二是学习教育的内容有待丰富。我们在市教育整顿领导小组的指导下拟定了方案,但是学习教育的内容主要还是“规定动作”的多,“自选动作”较少,教育形式、载体、种类都不够丰富。三是学习教育的成效有待凸显。有的纪检监察干部忙于各种工作,集体学习多、个人自学少,被动学习多、主动学习少,导致学习教育的目的没有完全实现,效果没有达到预期要求。三、下一步工作计划一是总结提升,确保请示报告到位。对于学习教育阶段好的做法,及时梳理、归纳、总结、提升,为下一步的学习教育积累经验。对于存在的问题,及时查缺补漏,及时整改完善,确保学习教育应有的成效。同时,落实请示报告制度,及时向市里请示报告工作开展情况,争取获得最大的支持。
- 下载

XX区教育局 2024 年上半年工作总结和下半年工作计划
目前,项目正在进行招标,7月份全面开工建设,确保9月秋季开学之前竣工并投入使用。统筹实施新建学校设备采购。投入资金1983万元为东平路小学、枫林小学、十六中、常青藤小学等12所中小学校和高速时代御府幼儿园、李洼幼儿园等7所新建幼儿园采购办公设备,目前项目意向公开已结束,招标正在进行中。(三)优化服务保障,形成良好教育生态一是做好教师队伍建设。完成第一批初级中学、小学、幼儿园教师资格认定工作,已有301人通过认定,第二批认定工作正在进行中。计划面向社会引进急需紧缺人才12人,招聘中小学新任教师60人,招聘农村特岗教师69人。目前,各层次招聘工作正按照程序有序进行。先后交流了校(园)长5人,提拔重用干部12人。二是做好民生保障。各类教育资助序时发放完毕。2024年春季学期共计受助学生27029人,资助资金1972.95万元。
- 下载








