北师大初中八年级数学下册第一章复习教案
-
- 页数:7页
- 字数:约 2557 字
- 大小:92.50KB
- 格式:.doc
- 版本:Office2016及以上版本
- 作者:白家安毓设计
第一章三角形的证明复习教案

教学课题
三角形的证明回顾与思考
设计者
课时安排
设计日期
教学目标
1.知识目标:在回顾与思考中建立本章的知识框架图,复习有关定理的探索与证明,证明的思路和方法,尺规作图等.
2.能力目标:进一步体会证明的必要性,发展学生的初步的演绎推理能力;进一步掌握综合法的证明方法,结合实例体会反证法的含义;提高学生用规范的数学语言表达论证过程的能力.
3.情感价值观要求
通过积极参与数学学习活动,对数学的证明产生好奇心和求知欲,培养学生合作交流的能力,以及独立思考的良好学习习惯.
教学重难点
重点:通过例题的讲解和课堂练习对所学知识进行复习巩固
难点:本章知识的综合性应用。
教学准备
教学流程
修改建议
考点1 等腰三角形的性质
1.已知等腰三角形的一个底角为80,则这个等腰三角形的
顶角为 ()
A.20 B.40 C.50 D.80
2.等腰三角形的两条边长分别为5 cm和6 cm,则它的周长是
_______________.
3.已知等腰三角形ABC的腰AB=AC=10 cm,底边BC=12 cm,
则△ABC的角平分线AD的长是________ cm.
归纳总结:
1)性质:
①等腰三角形的 两底角 相等。(“等边对等角”)
②等腰三角形的顶角平分线、底边上的中线、底边上的高线 互相重合 (三线合一)。
(2)判定:
①有两边相等的三角形是等腰三角形.
②有两个角相等的三角形是等腰三角形(等角对等边).
考点2等边三角形的性质
1.边长为6 cm的等边三角形中,其一边上高的长度为
________.
2.如图,已知△ABC是等边三角形,点B,C,D,E在同一直线上,且CG=CD,DF=DE,则∠E=________度.
【归纳总结】
(1)定义: 三条边都相等 的三角形是等边三角形。
(2)性质:
①三个内角都等于60度,三条边都相等
②具有等腰三角形的一切性质。
(3)判定:
①三个角都相等的三角形是等边三角形。
②有一个角等于60度的等腰三角形是等边三角形。
考点3 直角三角形
1.在Rt△ABC中,∠ACB=90,AB=10,CD是AB边上的中线,则CD的长是 ()
A.20 B.10 C.5 D.
2.在△ABC中,∠C=90,∠ABC=60,BD平分∠ABC交AC于点D,若AD=6,则CD=_____.
3.如图,△ABC中,∠C=90,AC=3,∠B=30,点P是BC边上的动点,则AP长不可能是 ()
A.3.5 B.4.2
C.5.8 D.7
【归纳总结】
(1)性质:直角三角形的两锐角互余。
(2)定理:直角三角形中,如果一个锐角是30度,那么它所对的直角边等于斜边的一半。
(3)定理:在直角三角中,斜边上的中线等于斜边的一半.
(3)判定:
有两个角互余的三角形是直角三角形
考点4 勾股定理及其逆定理
2.下列每一组数据中的三个数值分别为三角形的三边长,不能构成直角三角形的是 ()
A.3,4,5 B.6,8,10
C.,2, D.5,12,13
【归纳总结】
勾股定理:直角三角形两条直角边的平方和等于斜边的平方。
勾股定理的逆定理:如果三角形两边的平方和等于第三边的平方,那么这个三角形是直角三角形。
考点5 角平分线的性质和判定
1、如图,在△ABC中,∠C=90,∠BAC的平分线交BC于点D,若CD=4,则点D到AB的距离是________.
2.如图1-2,点D在BC上,DE⊥AB,DF⊥AC,且DE=DF,则线段AD是△ABC的 ()
A.垂直平分线 B.角平分线
C.高 D.中线
【归纳总结】
(1)角平分线上的点到这个叫的两边的距离相等。
(2)在一个角的内部,到角的两边距离相等的点在这个角的平分线上。
考点6 垂直平分线的性质和判定
2、如图,在△ABC中∠B=30
,BC的垂直平分线交AB于E,垂足为D.若ED=5,则CE的长为()
A.10 B.8 C.5 D2.5
2、如图,在Rt△ABC中,有∠ABC=90,DE是AC的垂直平分线,交AC于点D,交BC于点E,∠BAE=20,则∠C=_________.
【归纳总结】
(1)线段的垂直平分线上的点到这条线段的两个端点的距离相等
(2)到一条线段两个端点距离相等的点,在这条线段的垂直平分线上
考点7命题及逆命题
1、下列命题的逆命题是真命题的是()
A.如果a>0,b>0,则a+b>0
B.直角都相等
C.两直线平行,同位角相等
D.若a=6,则|a|=|b|
【归纳总结】
命题和逆命题:
命题:由条件和结论组成
逆命题:由结论和条件组成
考点7反证法
1、用反证法证明命题“三角形中必有一个内角小于或等于60”时,首先应假设这个三角形中___.
【归纳总结】
反证法:
先假设命题的结论不成立,然后推导出与已知条件相矛盾的结果
考点8三角形的全等
1.如图,△ABC,△CDE是等边三角形(1)求证:AE=BD
(2)若BD和AC交于点M,AE和CD交于点N,求证:CM=CN
(3)连结MN,猜想MN与BE的位置关系.并加以证明
您可能喜欢的文档
查看更多
北师大初中九年级数学下册第一章复习教案
- 页数:8页
- |大小:1M

北师大初中七年级数学上册第一章复习教案
- 页数:4页
- |大小:142.00KB

北师大初中八年级数学下册第二章复习教案
- 页数:3页
- |大小:50.00KB

北师大初中八年级数学下册第五章复习教案
- 页数:9页
- |大小:81.00KB
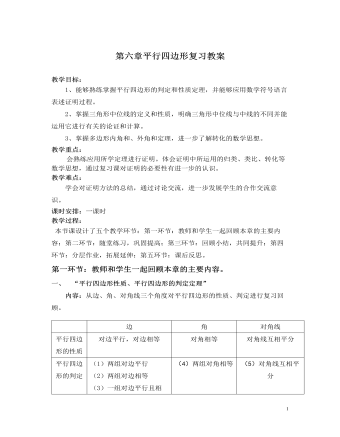
北师大初中八年级数学下册第六章复习教案
- 页数:5页
- |大小:96.00KB

北师大初中八年级数学下册第四章复习教案
- 页数:6页
- |大小:227.00KB
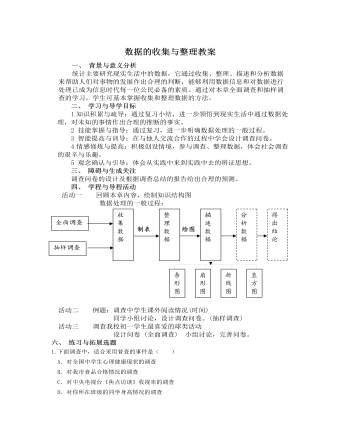
北师大初中七年级数学上册第六章复习教案
- 页数:7页
- |大小:517.00KB
热门课件教案

精选高中生期末评语
- 页数:42页
- |大小:7M
- 课件教案

音乐兴趣小组教案
- 页数:5页
- |大小:89.58KB
- 课件教案

部编版语文八年级下册《时间的脚印》教案
- 页数:4页
- |大小:511.50KB
- 课件教案

部编版小学语文一年级下册第16课《要下雨了》优秀教案范文
- 页数:4页
- |大小:19.94KB
- 课件教案

《我的未来不是梦》教案
- 页数:3页
- |大小:30.50KB
- 课件教案

部编版语文八年级下册《社戏》教案
- 页数:8页
- |大小:340.00KB
- 课件教案
今日更新

精选高中生期末评语
- 页数:42页
- |大小:7M

××县招商局2024年上半年工作总结
- 页数:12页
- |大小:142.54KB

“四零”承诺服务创建工作总结
- 页数:5页
- |大小:39.83KB

“改作风、提效能”专项行动工作总结
- 页数:6页
- |大小:139.05KB

“大学习、大讨论、大调研”活动情况总结报告
- 页数:7页
- |大小:26.12KB

2024年度工作计划汇编(18篇)
- 页数:72页
- |大小:196.93KB





